目录
1.反向传播
反向传播是利用链式法则 ,递归计算梯度的方法
2.分段反向传播求梯度 (重点)
不需要关于输入变量的明确的函数来计算导数,因为需要求的是梯度值。只需要将表达式分成不同的可以求导的模块,然后在反向传播中一步一步地计算梯度。
3.加法、乘法和取最大值在反向传播中关于梯度的理解
4.用向量化计算梯度
一、反向传播
反向传播是利用链式法则递归计算表达式的梯度的方法,链式法则是指用相乘将梯度表达式链接起来。
二、分段反向传播求梯度
不需要关于输入变量的明确的函数来计算导数,需要求的是梯度值。
分段计算是指将函数分成不同的模块,这样计算局部梯度相对容易,然后基于链式法则将其“链”起来。实际上并不需要关于输入变量的明确的函数来计算导数,只需要将表达式分成不同的可以求导的模块,然后在反向传播中一步一步地计算梯度。
假设有如下函数:
(1)前向传播计算每个门的输出:
1 | x = 3 # 例子数值 |
前向传播时创建了多个中间变量,每个都是比较简单的表达式,它们计算局部梯度的方法是已知的。当对前向传播时产生每个变量(sigy, num, sigx, xpy, xpysqr, den, invden)进行回传。我们会有同样数量的变量,但是都以d开头,需要存储对应变量的梯度。然后根据使用链式法则乘以上游梯度。
(2)反向传播计算每个门的梯度:
1 | # 回传 f = num * invden |
(3)注意
对前向传播变量进行缓存:在计算反向传播时,前向传播过程中得到的一些中间变量非常有用。
变量在不同分支的梯度要累加:如果变量x,y在前向传播的表达式中出现多次,那么进行反向传播的时候就要非常小心,使用+=而不是=来累计这些变量的梯度(不然就会造成覆写)。如果变量在线路中分支走向不同的部分,那么梯度在回传的时候,就应该进行累加。看(3)理解。
三、加法、乘法和取最大值在反向传播中关于梯度的理解
神经网络中最常用的加法、乘法和取最大值这三个门单元,它们在反向传播过程中的行为都有非常简单的解释。
2[x\y+max(w,z)]
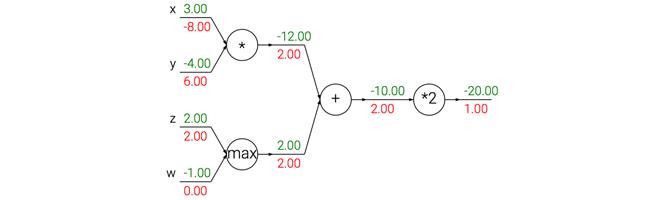
加法门单元:把输出的梯度相等地分发给它所有的输入。上例中,加法门把梯度2.00相等地路由给了两个输入。
取最大值门单元对:将输出梯度转给前向传播中值最大的那个输入,其余的输入的梯度为0。上例中,取最大值门将梯度2.00转给了z变量,因为z的值比w高,于是w的梯度保持为0。
乘法门单元:局部梯度就是交换之后的输入值,然后根据链式法则乘以输出值的梯度。上例中,x的梯度是-4.00x2.00=-8.00。
注意一种比较特殊的情况,如果乘法门单元的其中一个输入非常小,而另一个输入非常大,它将会把大的梯度分配给小的输入,把小的梯度分配给大的输入。这说明输入数据的大小对于权重梯度的大小有影响。例如,在计算过程中对所有输入数据样本乘以1000,那么权重的梯度将会增大1000倍,这样就必须降低学习率来弥补,所以数据预处理很重要。
