正向概率、逆向概率

根据表面现象，做出猜测

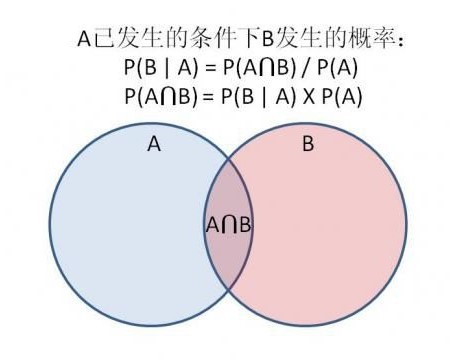
公式

P(B|A) = P(A|B)*P(B) / P(A)

实例一：拼写纠正

用户输入了一个不在字典的单词，猜测用户想输入的单词

P(猜测用户想输入的单词|用户实际输入的单词)

用户输入P(D)=“tha”，猜测用户想输入的可能是P(h1)=“the”、P(h2)=“than”……

一、公式理解

1.需要求出这些概率，将最大值作为预测的结果

P(h1|D)=P(猜测用户想输入的=“the”|用户实际输入的=“tha”)
P(h2|D)=P(猜测用户想输入的=“than”|用户实际输入的=“tha”)……

P(h|D)=P(D|h)*P(h)/P(D)

2.先验概率

P(h1)=P(猜测用户想输入的=“the”)
P(h2)=P(猜测用户想输入的=“than”) ……
即“the”、“than”的词频为先验概率

3.在某个猜想下，实际的概率

P(D|h1)=P(用户实际输入的=“tha”|猜测用户想输入的=“the”)
P(D|h2 )=P(用户实际输入的=“tha”|猜测用户想输入的=“than”)……

把“the”写成“tha”的概率，有很多衡量指标，可能与键盘中a和e的远近有关

二、模型比较理论

我们希望找出P(h1|D)、P(h2|D)…….中最大的作为预测结果，P(h|D)与P(D|h)*P(h)成正比，那么P(D|h)越大、或者P(h)越大对应的预测越大，越是我们需要的模型

1.最大似然估计((maximum likelihood estimation, MLE)

P(D|h)较大的模型较有优势

2.奥卡姆剃刀

P(h)较大的模型较有优势，即在实际中什么情况越常见，则其优势是越大的

实例二：垃圾邮件过滤

1.先验概率 P (h+)、P(h-)可以通过统计邮件库中垃圾邮件、正常邮件的比例来得到

2.P(D|h+)

将原始的条件概率通过以下几步化简

(1)P(D|h+)=P(d1,d2,d3…dn|h+)表示当这封邮件是垃圾邮件时，这封邮件中恰好出现D(d1,d2,d3…dn)中这N个单词的概率

(2)P(D|h+)=P(d1,d2,d3…dn|h+)=P(d1|h+)*P(d2|d1,h+)*P(d3|d1,d2,h
+)*…
对P(D|h+)条件概率可以展开为P(d1|h+)*P(d2|d1,h+)*P(d3|d1,d2,h
+)*…表示一封垃圾邮件第一个词为d1的概率，一封垃圾邮件第一个词为d1时第二个词为d2的概率，…

(3)朴素贝叶斯
假设di与di-1互不影响，即 特征独立
P(d1|h+)*P(d2|d1,h+)*P(d3|d1,d2,h
+)*…可以化简为P(d1|h+)*P(d2|h+)*P(d3|h
+)*…即只要统计垃圾邮件中d1、d2、d3的概率