PS：关于PCA数学推导，协方差矩阵、特征向量计算的那部分我就不放

一、降维

projection 高维到低维的 投影
highly redundant features 可以减少多余的特征

二、为什么需要降维

1.使用较少的计算机内存或磁盘空间（选择k，使得原数据的方差尽可能保留）
2.加快学习算法（选择k，使得原数据的方差尽可能保留）
3.可视化数据（选择k=2、3，将数据放在二维平面或三维空间展示）

三、PCA

1.PCA的理解

PCA就是找到一个低维的平面，把所有的数据都投射到该平面上时，使得投射误差 projection error 尽可能的小

n维降到k维，就是在n维空间中，找一个低维空间，该低维空间可以用k个n维的向量来表示，把所有的数据都投射到该空间中，使得投射的误差 projection error 尽可能的小

2.PCA需要计算

(1)用于降维的，k个n维的方向向量 U_redeuce
(2)数据在低维空间投影后的特征 Z

3.PCA实现步骤

4.PCA数学推导

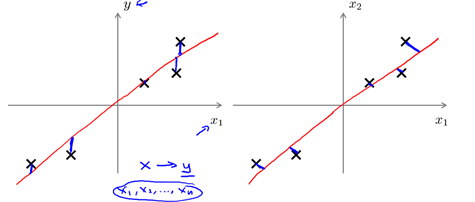
5.PCA与线性回归的区别

[右图] PCA最小化的是 投射误差（projection Error），不做预测
[左图] 线性回归最小化的是 预测误差，即预测结果与实际标签的距离

四、主成分个数k的选择

PCA的目的：是减少投射的平均均方误差

PCA的ｋ选取是：投射的平均均方误差与训练集方差的比例尽可能小的情况下，选择尽可能小的k
（这个比例小于1%，意味着原本数据的 方差有99%都保留下来了）

选取步骤：
1.令k=1，然后进行主要成分分析，获得前k个特征向量 U_reduce 和计算原数据 X 投影后的数据 Z
2.计算投射的平均均方误差与训练集方差的比例，是否小于1%
（如果不满足，令k=2，如此类推，直到找到可以使得比例小于1%的最小k值）

五、PCA不适合设防止过拟合

PCA并不是一个好的方法用来防止过拟合，防止过拟合，还是应该用正则化

原因：
1.PCA是无监督的，会 丢失与Y相关的信息
PCA是 无监督的，只关注输入数据X之间的相关性，降低数据Ｘ的维度，而不考虑标签Y，会让与Y有关的信息被丢失
对于监督学习，则寻找的是X与Y之间的联系

2.PCA会 丢失方差小的特征
PCA的假设是方差越大信息量越多，但是方差小的特征并不代表表对于标签没有意义